고정 헤더 영역
상세 컨텐츠
본문
1. Introduction
This technical report provides an overview of an image stitching, which is a fundamental technique used to create a panorama view by combining multiple overlapping images. The implementation uses affine transformation and bilinear interpolation, including transformation estimation, inverse warping, and blending. The process of image stitching consists of three key steps :
(1) We know at least 3 correspinding pixel between images →
(2) Then affine transformation is possible →
(3) Then all the pixel in one image can be moved in to other image = warping
2. Explanation of code
The overview of key steps of the code:
- Estimate affine transformation matrix.
- Perform forward warping to get p1, p2, p3, p4 and predict the entire size fo final image.
- Perform inverse warping with bilinear interpolation.
- Blend two images.
Detailed Explanation of the code:
- Read images and normalize pixel value
I1 = imread("stitchingL.jpg");
I2 = imread("stitchingR.jpg");
I1.convertTo(I1, CV_32FC3, 1.0 / 255);
I2.convertTo(I2, CV_32FC3, 1.0 / 255);
→ Convert the pixel values of both images from unsigned char format (0~255) to float format (0.0~1.0).
- 28 pair of corresponding pixels
// corresponding pixels
int ptl_x[28] = { 509, 558, 605, 649, 680, 689, 705, 730, 734, 768, 795, 802, 818, 837, 877, 889, 894, 902, 917, 924, 930, 948, 964, 969, 980, 988, 994, 998 };
int ptl_y[28] = { 528, 597, 581, 520, 526, 581, 587, 496, 506, 500, 342, 558, 499, 642, 474, 456, 451, 475, 530, 381, 472, 475, 426, 539, 329, 341, 492, 511 };
int ptr_x[28] = { 45, 89, 142, 194, 226, 230, 246, 279, 281, 314, 352, 345, 365, 372, 421, 434, 439, 446, 456, 472, 471, 488, 506, 503, 527, 532, 528, 531 };
int ptr_y[28] = { 488, 561, 544, 482, 490, 546, 552, 462, 471, 467, 313, 526, 468, 607, 445, 429, 424, 447, 500, 358, 446, 449, 403, 510, 312, 324, 466, 484 };- Calculate affine Matrix A12, A21
Mat A12 = cal_affine<float>(ptl_x, ptl_y, ptr_x, ptr_y, 28);
Mat A21 = cal_affine<float>(ptr_x, ptr_y, ptl_x, ptl_y, 28);
cal_affine()
- Estimate affine transformation matrix.
- Mx=b:
Mat M(2 * number_of_points, 6, CV_32F, Scalar(0));
Mat b(2 * number_of_points, 1, CV_32F);- Making 2 equation for single pair of corresponding pixel : M becomes 2N*6 matrix.
for (int i = 0; i < number_of_points; i++) {
M.at<T>(2 * i, 0) = ptl_x[i];
M.at<T>(2 * i, 1) = ptl_y[i];
M.at<T>(2 * i, 2) = 1;
M.at<T>(2 * i + 1, 3) = ptl_x[i];
M.at<T>(2 * i + 1, 4) = ptl_y[i];
M.at<T>(2 * i + 1, 5) = 1;
b.at<T>(2 * i) = ptr_x[i];
b.at<T>(2 * i + 1) = ptr_y[i];
}
So if we have 5 pair of corresponding pixel, number of unknown value is 6 and number of equation is 10. In this case, we define it as overdetermined system.
However, overdetermined system has a problem. If the number of unknown value is 2 and number of equation is 4, we cannot get the exact junction of 4 equations, while the exact junction exists if the number of equation is 2. As it can be seen in the figure below:
So, to solve the overdetermined system, we should find the center point which minimzes the error. This can be written as a mathematic formula:
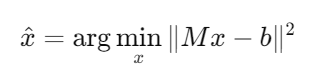
Using this formula, we can get solution x with the process below:
Since MTM becomes a square matrix, we can take its inverse and obtain a solution even if the original system was overdetermined. As a result, overdetermined system is changed to conventional linear system which is Ax=d.
- Least Squares Solution
→ This code directly implements the formula for computing x described above.
transpose(M, M_trans);
invert(M_trans * M, temp);
affineM = temp * M_trans * b;- Forward Warping
Transform the corner points of I2 into coordinate system of I1. Through this we can get p1, p2, p3, p4 and estimate the size of entire image.
Point2f p1(A21.at<float>(0) * 0 + A21.at<float>(1) * 0 + A21.at<float>(2), A21.at<float>(3) * 0 + A21.at<float>(4) * 0 + A21.at<float>(5));
Point2f p2(A21.at<float>(0) * 0 + A21.at<float>(1) * I2_row + A21.at<float>(2), A21.at<float>(3) * 0 + A21.at<float>(4) * I2_row + A21.at<float>(5));
Point2f p3(A21.at<float>(0) * I2_col + A21.at<float>(1) * I2_row + A21.at<float>(2), A21.at<float>(3) * I2_col + A21.at<float>(4) * I2_row + A21.at<float>(5));
Point2f p4(A21.at<float>(0) * I2_col + A21.at<float>(1) * 0 + A21.at<float>(2), A21.at<float>(3) * I2_col + A21.at<float>(4) * 0 + A21.at<float>(5
int bound_u = (int)round(min(0.0f, min(p1.y, p4.y)));
int bound_b = (int)round(max(I1_row-1, max(p2.y, p3.y)));
int bound_l = (int)round(min(0.0f, min(p1.x, p2.x)));
int bound_r = (int)round(max(I1_col-1, max(p3.x, p4.x)));- bound_u → upper bound (top) : The topmost y-coordinate between I1 and I2
- bound_b → bottom bound : The bottommost y-coordinate between I1 and I2
- bound_l → left bound : The leftmost x-coordinate
- bound_r → right bound : The rightmost x-coordinate
- Inverse warping with bilinear interpolation
For each pixel in the final image, we apply inverse warping. It computes where a pixel in the stitched image came from in I2 using A12 (I1 to I2). Since the warped coordinates are floating point, bilinear interpolation is used to compute the intensity.
for (int i = bound_u; i <= bound_b; i++) {
for (int j = bound_l; j <= bound_r; j++) {
float x = A12.at<float>(0) * j + A12.at<float>(1) * i + A12.at<float>(2) - bound_l;
float y = A12.at<float>(3) * j + A12.at<float>(4) * i + A12.at<float>(5) - bound_u;
float y1 = floor(y);
float y2 = ceil(y);
float x1 = floor(x);
float x2 = ceil(x);
float mu = y - y1;
float lambda = x - x1;
if (x1 >= 0 && x2 < I2_col && y1 >= 0 && y2 < I2_row)
I_f.at<Vec3f>(i - bound_u, j - bound_l) = lambda * (mu * I2.at<Vec3f>(y2, x2) + (1 - mu) * I2.at<Vec3f>(y1, x2)) +
(1 - lambda) *(mu * I2.at<Vec3f>(y2, x1) + (1 - mu) * I2.at<Vec3f>(y1, x1));
}
}
- Blending
To ensure a smooth transition between I1 and the warped I2, a basic linear blending technique is employed.
blend_stitching(I1, I2, I_f, bound_l, bound_u, 0.5);
blend_stitching()
- If both I1 and I2 have pixel values: apply alpha * I1 + (1 - alpha) * I2
- If only I1 is valid, use I1
- If only I2 is valid, use I2
void blend_stitching(const Mat I1, const Mat I2, Mat &I_f, int bound_l, int bound_u, float alpha) {
int col = I_f.cols;
int row = I_f.rows;
// I2 is already in I_f by inverse warping
for (int i = 0; i < I1.rows; i++) {
for (int j = 0; j < I1.cols; j++) {
bool cond_I2 = I_f.at<Vec3f>(i - bound_u, j - bound_l) != Vec3f(0, 0, 0) ? true : false;
if (cond_I2)
I_f.at<Vec3f>(i - bound_u, j - bound_l) = alpha * I1.at<Vec3f>(i, j) + (1 - alpha) * I_f.at<Vec3f>(i - bound_u, j - bound_l);
else
I_f.at<Vec3f>(i - bound_u, j - bound_l) = I1.at<Vec3f>(i, j);
}
}
}3. Experimental results
- Two input images are used, along with 28 manually annotated corresponding points. The affine transformation is calculated, and I2 is warped and aligned onto I1. The final result demonstrates successful alignment and seamless stitching.

'Computer Vision' 카테고리의 다른 글
| [Computer Vision] _ Image Rotation (0) | 2025.06.21 |
|---|---|
| [RL] _ Intro to RL (0) | 2024.09.02 |
| Computer Vision 2 _ Chap 07 (0) | 2024.09.02 |
| Computer Vision 2 _ Chap 06 (0) | 2024.09.02 |
| Computer Vision 2 _ Chap 05 (0) | 2024.09.02 |






댓글 영역